:تـقـديـم 

بدأت الرياضيات تستعمل في مرحلة صدر الإسلام على شكل معارف أو صيغ هندسية وحسابية تتيح حل المشاكل اليومية للناس بطرق مختلفة[1] وبما تقتضيه أحوالهم الطبيعية والاجتماعية العادية المتناسبة مع تشريعات الدين الإسلامي الجديد: كتحديد مواقيت الصلاة والمعاملات التجارية وقسمة المواريث وتحديد القبلة ورؤية الأهلة…إلخ.  فالقرآن الكريم المنزل على هذه الأمة هو أيضا استعمل اصطلاحات كثيرة تتصل باللغة الرياضية، كالإحصاء والتقدير والموازين والحساب والعدد والاستواء والتسطيح والتكوير بمشتقاتها العديدة، كما استعمل الأرقام الصحيحة بمراتبها كلها (الوحدات والعشرات والمئات والآلاف…) والأعداد الكسورية كالنصف والربع والخمس والسدس…إلخ.

 لكن صورة العلم الرياضي لم تبق محصورة بالتعاليم التقليدية داخل الحضارة العربية الإسلامية منذ مرحلة النشأة، بل تمكنت ـ بفضل تطور العلوم الإسلامية المختلفة والحاجات الحضارية الملحة، والثقافة العلمية المنفتحة، والترجمات الدقيقة للكتب الرياضية القديمة (سريانية، ويونانية، وهندية)، والعمل على دراستها دراسة علمية من قبل علماء جهابذة ـ مكنتهم من تجاوز ما كان موروثا والعمل على ترجمت كتب الأقدمين وإنتاج كتب علمية مهمة قدمت نظريات رياضية قيِّمة (كالجبر، والتحليل التوافقي، وعلم المثلثات….) احتلت بفضلها المدينةُ الإسلامية مكانة علمية عظيمة داخل الإرث الحضاري العالمي، مما جعلها تتفوق على مثيلاتها من الحضارات السابقة بِنَفَسٍ زائد من الإنتاج العلمي والعطاء المعرفي.

من بين العلماء المسلمين الكبار الذين أسهموا بإنتاجاتهم في العلوم الرياضية داخل البيئة الثقافية العربية الإسلامية، نذكر الرياضي المغربي الفذ، والطبيب المقتدر، الأندلسي الأصل أحمد ابن إبراهيم بن علي بن منعم العبدري، أبو جعفر المتوفى سنة 626هـ/1228م، صاحب كتاب “فـقـه الحسـاب“، الذي سيكون محط هذه النظرة العامة التي تُعرِّف بطبيعة هذا الكتاب، وتبرز أهم مضامينه العلمية، والمصادر والدراسات التي تحدثت عنه، وموقعه الريادي في تاريخ الرياضيات بشكل خاص.

• التعريف بالمؤَلَّف:
• طبيعة الشكل المؤَلَّف:

تعتبر هذه النسخة من كتاب “فقه الحساب”، الذي يعود تأليفه إلى العالم الرياضي المغاربي ابن منعم العبدري[2]، هي النسخة الوحيدة والفريدة التي وجدها الأستاذ الباحث ادريس لمرابط سنة 1981 في كنف الخزانة الوطنية بالرباط. وهي ضمن المجموع الذي رقمه 416، والذي كان موجودا بخزانة زاوية تمكروت جنوب المغرب، صفحاتها مرقمة من 214 إلى 419، مكتوبة بخط مغربي وسطي سنة 958هـ/1551م، بمدينة تونس على يد حسن الربعي، وهي لا تزال على حالها محفوظة حفظا جيدا رغم وجود بياض في أمكنة متعددة، مسطرتها: 28، وفي كل سطر 12 كلمة تقريبا[3].

يتضمن الكتاب مقدمة تبرر الغرض من تأليفه، وبيان أهمية موضوعه (أي علم الحساب) وذكر معنى التحليل والتركيب المعتمدين في البراهين على بعض القضايا الرياضية، ثم الإعتماد على المصادر التي ينبغي مراجعتها قبل قراءة الجانب النظري و العلمي من الكتاب، يذكرمنها مصدرين أسايين هما: كتاب “الأصول” أقليدس وفصل من كتاب “الاستكمال” للمؤتمن بن هود.  في الختام يقسم مضامين هذا الكتاب تقسيما منهجيا ويضعهما في بابين رئيسين: الأول يعكس تصور علمي نظري، والثاني يسير في اتجاه عملي تطبيقي.

الباب الأول: في العدد الصحيح، وهو  ينقسم بنظريّه وعمليّه وتصانيفه، وحصر وجوه أعماله إلى أحد عشر نوعا:

• النوع الأول: في مراتب العدد وأسمائه،
• النوع الثاني: في صور الغبار وتصريفه على منازل العدد،
• النوع الثالث: في جمع الأعداد بعضها إلى بعض،
• النوع الرابع: في طرح الأعداد بعضها من بعض،
• النوع الخامس: في ضرب الأعداد،
• النوع السادس: في القسمة،
• النوع السابع: في أخذ أضلاع الأعداد المربعات والمكعبات والمخمسات والمسبعات وما أشبه ذلك،
• النوع الثامن: في خواص الأعداد المتوالية، وعلل جميع أزواجها وأفرادها ومربعاتها ومكعباتها
• النوع التاسع: في الأشكال العددية،
• النوع العاشر: في وجود العدد التام والزائد والناقص والأعداد المتحابة،
• النوع الحادي عشر: في الكلمات التي لا يتكلم فيها البشر إلا بإحداهن، وفيه يقدم التحليل التوافقي وتطبيقاته على المعجم اللغوي.

الباب الثاني: في الكسور وأحكامها، يحتوي على وجوه معانيه وأعماله، وعلى علميّه وعمليّه، وينقسم إلى أربعة أنواع:

النوع الأول جعله المؤلف في بسط الكسر المتصل،

النوع الثاني في بسط الكسر المنفصل،

النوع الثالث في بسط الكسر المبعَّض،

النوع الرابع في بسط الكسر المشترك.

ثم يذيل هذا الباب بذكر أنواع التصريف، وفصول تتعلق بمسائل من الجبر والحط وأخذ أضلاع أشكال الكسر، ليختم الكتاب بمائل من ملح علم الحساب.

وأما عمل المحقق في هذا الكتاب، فهو محدود بسبب فرادة النسخة التي اعتمدها كما نص بنفسه على ذلك[4]، حيث اكتفى بوضع مقدمة مختصرة تتضمن: تعريفا مركزا بصاحب الكتاب، ونظرة سريعة على النسخة المعتمدة تشتمل على وصف المخطوطة، وأبواب الكتاب، وطرق البرهان فيه، وفقرات جد مختصرة تشير إلى الأهمية العلمية للكتاب في كلامه عن الأعداد والحساب، وفي التحليل التوافقي في فقه الحساب، وفي حساب الجذور بالتقريب، وفي الخطوة المهمة التي حققها ابن منعم نحو الاستدلال بالترجع.

وقد أضاف المحقق في هذا الكتاب ترجمات لمجموعة من القضايا الرياضية المدرجة في “فقه الحساب” من اللغة الطبيعية إلى اللغة الرمزية المعاصرة. ومن هذه القضايا على سبيل المثال:

– القضية 9.8.1 “إذا كانت الأعداد متوالية من الواحد إلى عدد مفروض جمعت إلى عدد آخر مجموع على التوالي من الواحد إلى عدد يتلو العدد المفروض، فإن المُجْتَمِع يكون مربعّا ضلعه أعظم عدد من الأعداد المتوالية”[5].

تتخذ هذه القضية الرياضية صورتها الرمزية على الشكل التالي:

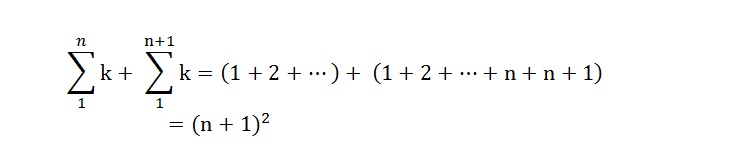
 القضية 33.8.1 ” إذا توالت أعداد من الواحد كم كانت، فإن مجموع مربعاتها على التوالي مساوٍ لثلث مكعب أعظم الأعداد التي فيها مع نصف مربَّع أعظم الأعداد [ و ]*مع سدسه أيضا[6].

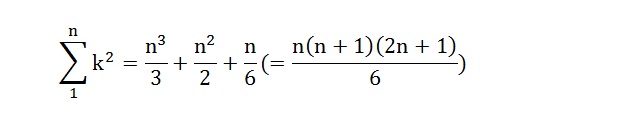
كما نجد أيضا أن المحقق أقدم على ترجمة بعض الصيغ الرياضية لحساب الجذور بالتقريب، كان لابن منعم الدور الأبرز في اقتراحها، حيث لم يوجد لها أثر خارج نطاق الغرب الإسلامي[7].

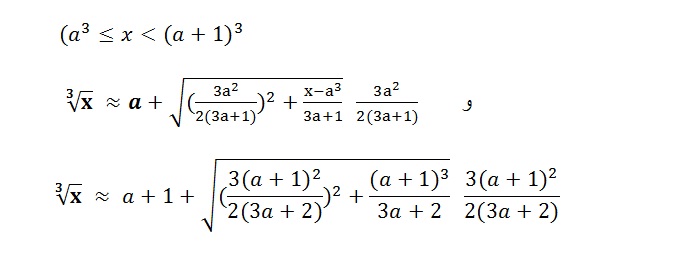
أما على مستوى متن هذا الكتاب، نجده تطفوا عليه مجموعات من التصويبات تتخذ شكل إضافات وشروحات توسع عبرها مضمون كتاب “فقه الحساب” كما وكيفا:

– على مستوى الكم: نلاحظ أن المحقق وضع مجموعة من التصحيحات الهامة على الكلمات الغامضة في النص، من أجل توضيح السياق الصحيح والمحدد لمعنى الجمل. ومن هذه الكلمات نذكر  على سبيل المثال:

” من اهتبل” الكلمة الصحيحة والمكملة لمعنى الجملة في النص “الاهتبال”[8].

” الأوطاطيقيون” الكلمة الصحيحة والمكملة لمعنى الجملة في النص ” الأرطماطيقيون”[9].

ثانيا: نلاحظ أن المحقق أبان في هامش الكتاب على أسماء بعض الخلفاء والعلماء الرياضيين اللذين ذكرهم ابن منعم في “فقه الحساب”، ومن هؤلاء: المهدي بن تومرت[10](ت. 1130) مؤسس الدولة الموحدية، والناصر أبو عبد الله محمد بن يعقوب المنصور[11](1199-1213م) رابع الخلفاء الموحدين، والمؤتمن بن هود[12](478هـ/1086م) الملك الرياضي وصاحب كتاب الاستكمال، وأقليدس الإسكندراني[13](نحو330-نحو 275ق.م) العالم الرياضي الكبير ومؤسس مدرسة الرياضيات بالإسكندرية وصاحب كتاب “الأصول”، وابن سيد المهندس[14](كان حيا سنة 1086) العالم الرياضي الأندلسي، وعبد الله بن عياش الحصار[15]، صاحب كتاب ” البيان والتذكار في علم مسائل الغبار”.

– على مستوى الكيف: سَاوَرَ فيه المحقق طرح مجموعة من التعاريف لبعض المفاهيم والأعمال الرياضية، على اعتبار أن هذه الأخيرة بمثابة مفاتيح تسهل عملية فهم واستيعاب أهم القضايا الرياضية المتمركزة في مضمون الكتاب، وطبيعة اللغة المتداولة بها. ومن من هذه المفاهيم والأعمال المستدرجة والمشروحة في هامش الكتاب كلمة الأُس[16]، وحروف الغبار[17] ونظام الحساب الرومي[18]… إلخ.

أنهى المحقق صفحات “فقه الحساب” بأصناف مختلفة من المصادر والمراجع العربية وغير العربية، و وضع صفحات مصورة من مخطوط الكتاب[19]، وفهرسا عاما، إضافيا لكلمة المفاتيح والأعمال والأعلام…إلخ، ليختتم هذا الكتاب بمقدمة باللغة الإنجليزية يترجم فيها المحقق أبرز العناوين الفرعية من القسم الأول “ابن منعم وكتابه “فقه الحساب” المكتوبة باللغة العربية.

• طبيعة مضمون المؤَلَّف:

إن كتاب (فقه الحساب) نراه يعالج على مستوى طبيعة مضمونه وبالخصوص في الباب الأول في الصحيح أحد عشر نوعا من علم العدد، من أجودها العمليات الحسابية الأربع ( القسمة ـ الجمع ـ الطرح ـ الضرب) ثم كذلك الأعداد المتحابة والأعداد التامة بالإضافة إلى خواص مجاميع الأعداد والكسور، ثم البحث في طرق إيجاد الجذور من الرتب الكيفية.[20] كما نلاحظ أنه اهتم كثيرا في هذا الباب من هذا الكتاب على استخراج الجذور، إذ لم يكتف بالتطرق إلى الجذور التربيعية والتكعيبية بل راح يحسب جذورا من رتب أعلى، مثل الجذر الخماسي للعدد 248832 والجذر السباعي للعدد 35831808 مؤكدا بأن هذه الطريقة تُمكن من استخراج جميع الجذور مهما كانت مراتبها.

أما بخصوص الباب الثاني من هذا الكتاب والذي خصصه في الجزء العملي من الحساب في الكسور وأحكامها، والذي قسمه إلى أربعة أنواع : النوع الأول حدده في بسط الكسر المتصل والنوع الثاني في الكسر المنفصل والنوع الثالث في بسط الكسر المبعض والنوع الرابع في بسط الكسر المشترك، وهو في هذا الاتجاه نراه يقول في مقدمة هذا الباب أي باب الحساب في الكسور وأحكامها، “أنه بالنسبة للكسر إما أن يكون متصل، وإما منفصل، وإما مبعض ويسمى المؤلَّف، وإما مشترك وهو ما تركب عن هذه. فالكسر يدور على هذه الأنواع الأربعة ولكل نوع منه حكم”[21] له مجال يحدده.

ومن أهم ما يتميز به هذا الكتاب عن كثير من الكتب الرياضية المغاربية، نجده يعطي الأهمية الكبيرة للبرهان الرياضي الذي وضفه في أغلب القضايا الرياضية[22] هذا البرهان الرياضي الذي يتمثل في كل من البرهانين التحليلي والتركيبي[23] الذين يِنِّمَانِ عن فعالية العقل الرياضي الحسابي وطاقته الإبداعية.

ومن أفضل ما تطرق إليه هذا العالم الرياضي المغربي الكبير في كتابه “فقه الحساب” رغم جهل بعض الأوساط العلمية لانتاجاته العلمية في مجال العلوم الرياضية، هو اهتمامه البالغ بالتحليل التوافقي. ويشير في هذا السياق ابن منعم في مقدمة النوع الحادي عشر من الباب الأول في هذا الكتاب، أن علماء اللغة قد اهتموا بالتحليل التوافقي، لعلاقته الوطيدة بعلم النطقيات والمعجميات وعلم التعمية.[24] ومن أبرز الذين كان لهم اهتمام بارز في هذا الموضوع، نجد العالم اللغوي الكبير الخليل ابن أحمد الفراهيدي، (٧۱٨/٧٨٦م) الذي استعان بحساب الترتيبات والتوافيق من أجل تأسيس علم المعاجم العربية لإرساء قواعد علمية تسيِّر هذا العلم، وبهذا نجد ابن منعم يواصل ما بدأه هذا العالم في كتاب “فقه الحساب” بالقول: و”الخليل رحمة الله إنما ذكره عدة أوضاع الكلمات التي لا يتكرر فيها حرف فقط…[25]. وعلى هذا الأساس يوضح ابن منعم الإطار العام لدراسته تماشيا على نهج أسلافه باستعماله لحساب الترتيبات والتوافق بطرق تجديدية، بحيث يقول “وليكن اصطلاحنا في مثالنا هذا في عدّة حروف أبجد أن يكون ثمانية وعشرين، وأن تكون أكبر كلمة من عشرة أحرف بالزوائد والتكرير، مثل أرسطوطاليس-خ، وأن يتعاقب على الحرف الواحد ثلاث حركات وساكن، وأن لا يبدأ بساكن، ويتوالى ساكنان”[26].

من الواضح أن الغرض الهام الذي دفع ابن منعم العبدري إلى تأليف هذا الكتاب كما يقول بنفسه: هو “توضيح الغامض وجمع المشتت من علم الحساب”. مما حذي به في النهاية إلى وضع تصنيف عام لجل كتب الأقدمين في علم الحساب التي اضطلع عليها بعد قراءة علمية دقيقة، وسواها في أربعة أصناف معينة وهي كالتالي:

– الكتب التي تتناول الجانب النظري دون غيرِه.

– الكتب التي تتناول الجانب التطبيقي دون غيره.

– الكتب التي نجد فيها محاولات دمج الجانبيين النظري والتطبيقي.

– الكتب التي تتضمن مسائل غريبة ونادرة دون توضيح حلولها وبراهينها.[27]

2. مصادر دراسة ابن منعم

لم تأخذ شخصية ابن منعم العبدري حقها من التعريف والدراسة في جل المصادر التاريخية سواء القديمة منها أو الحديثة كما يجب، ولم يعتني أغلب المترجمون والمفهرسون والمهتمون بتاريخ العلوم سواء المحدثون منهم والمعاصرون في مؤلفاتهم عن السمة الذاتية والموضوعية لهذه الشخصية العملاقة في الغرب الإسلامي. لكن في نفس الوقت لا يمكن أن نغض النظر عن بعض المصادر التاريخية، رغم أنها محصورة في عدد معين، وأيضا عن بعض الدراسات الحديثة التي قام بها زبدة من الباحثين الكبار عن أعماله وإنجازاته الرياضية. و بهذا سنعمل على سرد هذه المصادر القديمة والمراجع الحديثة التي تكلمت عن شخصيته بالذات.

• مصادر قديمة

عرفت بعض المصادر وكتب التراجم مكانة قيمة في تاريخ العلوم، والتي بواسطتها اتخذت شخصية ابن منعم مكانها من البحث عند مؤرخي العلوم، ومنطلقا هاما للدراسة والبحث عن أهم إنجازاته العلمية.

والملاحظ أنه من بين المصادر الأولى المصنفة ضمن كتب التراجم والأعلام، والتي أعطت لهذا العَلَم المغاربي حقه في السياقين التاريخي والعلمي، نجد كتاب “الذيل والتكملة”[28] لابن عبد الملك المراكشي، الذي قدر مكانة هذا العالم في عصره وبيّن موطنه الأصلي والمدينة التي استقر فيها والاهتمامات التي شغلها والاضافات العلمية التي ساهم بها، والجماعة التي أخذت عنه كل ما أنتج في العلوم العددية والهندسية.

وقد تجدد ذكر ابن منعم من بعد عبد الملك المراكشي عند كل من ابن هيدور التادلي في مؤلفه “تحفة الطلاب وأمنية الحساب في شرح ما أشكل من رفع الحجاب”[29]. وعند ابن خلدون في المقدمة[30]، وحاجي خليفة في كتابه “كشف الظنون”[31] من غير إشارة إلى حياته وأعماله أو تفاصيل عنها.

• مراجع حديثة:

 ساهمت مجموعة من الدراسات التي قام بها بعض الباحثين المتخصصين في مجال تاريخ العلوم، استحضار دور و مكانة علماء الغرب الإسلامي في تطور المعارف العلمية بشتى أنواعها. وقد كان لهذه الأبحاث دورًا مهما تموقعت من خلاله شخصية ابن منعم العبدري كأعظم رياضي عرفته منطقة الغرب الإسلامي مابين القرن الثاني عشر والثالث عشر الميلادي.

من بين الدراسات الأولى التي أشارت إلى شخصية بن منعم وإلى أهم إنجازاته الرياضية، هي تلك التي قام بها مؤرخ الرياضيات المغربي ادريس لمرابط في كتابه (مدخل إلى تاريخ الرياضيات بالمغرب العربي) ، ثم أعمال كل من الباحثين أحمد جبار ومحمد أبلاغ المنجزة حول تاريخ الرياضيات في الغرب الإسلامي[32]، التي نجد في جلها بصمات للعالم الرياضي ابن منعم العبدري سواء بواسطة إشارات بينية لمكانته العلمية وللحقبة الزمنية التي أنتج فيها أعماله الرياضية، أو بطريقة تحليلية شارحة لأهم إنجازاته في العلوم العددية والهندسية.

 وتماشيا على أعمال هؤلاء، نستقرأ في مؤلفات أحد الباحثين السائرين على نفس الدرب في مجال تاريخ العلوم، ذكره لهذا العَلَم الرياضي المغاربي، أنه كان صاحب الفضل الكبير في تطوير التحليل التوافقي وممثل للإتجاه الإبداعي[33] الذي انطلقت بوادره مع أواخر القرن السادس الهجري (ق12م).

• الدراسات المنجزة عن مضمون كتاب فقه الحساب:

أسهم الرياضي ابن منعم في تطوير الخوارزميات الحسابية (القسمة واستخراج الجذور…الخ) والحساب التوافقي ونظرية الأعداد، مما حدا بخيرة من الباحثين المتخصصين في هذا الجانب العلمي الدقيق، دراسة وفحص المسائل والبراهين الإستقرائية التي وضعها ابن منعم كحلول رياضية توافقية تجاوزت موضوعيا ما كان مألوفا من قبل.

فجل الدراسات التي تقدم بها كل من أحمد جبار ومحمد أبلاغ، تظهر أن التحليل التوافقي[34] الذي تجلى ميلاده في الدور الذي ساهم به علم اللغة مَلِيًّا، والذي كان بمثابة الأصل[35] المُمَهِد لهذا الفرع الرياضي، قد عرف تطورا بارزا مع ابن منعم و ابن البنا وتلامذته لاحقا. فعلى الرغم من إغفال بعض الدراسات لأعماله في هذا الجانب، كما لاحظ محقق  كتاب ابن هيدور التادلي “التمحيص في شرح التلخيص” على “أن التحليل التوافقي كان مظهرا آخر من مظاهر التجديد في نظرية الأعداد خاصة والفكر الرياضي عامة، ولاحظ أن هذا البعد التجديدي الذي درسه رشدي راشد في تاريخ الرياضيات العربية “بين الجبر والحساب” قد ركز فيه على المدرسة الشرقية وأهمل الإسهام المغربي الذي افتتحه ابن منعم في “فقه الحساب” وهو ما استدركه كل من أحمد جبار ومحمد أبلاغ”[36] بعد ذلك، فجاءت أبحاثهم مبرزة ومكملة لهذا الطابع التجديدي في رياضيات علماء الغرب الإسلامي، و خاصة لدى ابن منعم العبدري في مجال التحليل التوافقي.

• إسهاماته و تأثيره في تاريخ الرياضيات:

جسد هذا الكتاب حضورا بارزا في تاريخ الرياضيات، بوضعه لدراسة مكملة ومجددة لعلم الحساب الرياضي. ومن بين أهم ما نجده من الإسهامات التي توصل إليه ابن منعم العبدري في ميدان الحساب التآلفي combinatoire، هو وضعه لخاصيات رياضية غير مسبوقة والتي لا نجدها في إسهامات الرياضيين الكبار الذين سبقوه مثل الخيام (ت1131م) والكرجي (ت 1020م ) وديوفنطس الإسكندراني (ت ما بين سنة 200 و 214 قبل الميلاد) والسموؤل المغربي (ت 1174م). ومن هذه الإسهامات الواردة في كتاب “فقه الحساب”، كما يذكر الباحث المغربي إدريس لمرابط في “مدخل إلى تاريخ الرياضيات في المغرب العربي” نجد الصيغة التالية[37]:وفي سياق الإسهامات العلمية أيضا لهذا العالم الرياضي الكبير ، نجد المثلث الحسابي المعروف بمثلث باسكال (١٦٢٣ـ ١٦٦٢) المتداول في الكتب المدرسية والذي يؤدي دورا مهما في التحليل التوافقي والذي كان من قبل ينسب إلى الرياضي الصيني شو شي كيي ( ت.1303)، ثم اكتشف في الأعمال الرياضية عند الكرجي429) هـ/1020م([38] فيما بعد.

لقد أثبتت الدراسات الابستمولوجية أن ابن منعم العبدري كان له الدور الأهم في إنشاء واستخدام هذا المثلث في عدة مجالات رياضية، ويؤكد في هذا الصدد الباحث الجزائري أحمد جبار في كتابه “العلوم العربية في عصرها الذهبي”L’age d’or des Sciences Arabes” أن هناك أعمال أصيلة قام بها الرياضي المراكشي ابن منعم العبدري في كتابه ” فقه الحساب ” الذي خصص له بابا كاملا لعرض الأعمال والصناعات التي يمكن حصرها في كلمات للغة معطاة، لقد كان عليه ليصل إلى هذه النتائج أن يشيد المثلث الحسابي وهو جدول الأعداد المستعمل اليوم في عدة مجالات رياضية والذي يحمل اسم “مثلث باسكال” الذي أعطى النتائج الانتقالية التي شكلت فيما بعد بكثير الأدوات الأولى في التحليل التوافقي[39].

وقد كان لهذا الكتاب أيضا تأثير عميق على كبار الرياضيين المغاربة والأندلسيون الذين أتوا من بعده، نذكر من بين هؤلاء: الرياضي المراكشي ابن البنا (ت. 1321م) صاحب كتاب “رفع الحجاب عن وجوه أعمال الحساب” وتلميذه ابن هيدور التادلي (ت. 1413م) الذي ساهم في شرح جل كتب أستاذه الرياضية، والأندلسي ابن زكريا الغرناطي (ت. 1404) مؤلف كتاب “حط النقاب بعد رفع الحجاب عن وجوه أعمال الحساب”.

خـاتمـة:

   الخلاصة التي نختم بها هذا المقال، هي أن المؤلف حاول في كتابه “فقه الحساب” ومن خلال دراسته لعلم العدد دراسة تاريخية وعلمية، نجده عمل على وضع مجموعة من الخاصيات الرياضية الممكنة للمساهمة في تطوير هذا العلم من الناحية النظرية ( العلمية )، وكذا تبسيط وتسهيل العمليات الحسابية للمتخصصين في هذا العلم من الناحية التطبيقية ( العملية ).

ومن أهم المزايا التي يطرحها هذا الكتاب نجد أن صاحبه لا يثير قضايا ذات طابع فلسفي حول وضع الأعداد وما لانهاية، إدراكاً منه النهوض بهذا العلم تدقيقا، وإضفاء عليه ما توصلت إليه قريحته من صيغ رياضية تنظيما، ليصبح هذا الفرع العلمي متفردا داخل نسق رياضي مبني على مبادئ أولية تتخذ شكل خاصيات، للوصول إلى نتائج تعكس بشكل صحيح هذه المنطلقات والمبادئ.

إن الهدف الذي كان من وراء هذه الإنجازات الرياضية بالنسبة لعلماء الغرب الإسلامي، هو أولا: توضيح ما كان مستعصيا على الفهم عند بعض الرياضيين القدامى، خصوصا فيما يتعلق ببعض النظريات الرياضية والطرق المستعملة، ثم ثانيا: القضاء على العقلية النمطية المحافظة على نفس البنية التحليلية والتركيبية للنظريات الرياضية، التي هي في الأصل مبنية على الخصوبة والاحتمالات المنطقية.

المصادر و المراجع المعتمدة:

• ابن منعم، فقه الحساب، بتقديم د. إدريس لمرابط، دار الأمان، الرباط، 1426/2005م.
• ابن عبد الملك المراكشي، الذيل والتكملة، السفر الأول، تحقيق محمد بن شريفة، دار الثقافة، بيروت، (د.ت)، السفر 1، القسم الأول.
• ابن خلدون، عبد الرحمن، المقدمة، حققها وقدم لها وعلق عليها عبد السلام الشدادي، 5مج، خزانة ابن خلدون بيت الفنون والعلوم والآداب، 2005.
• أبلاغ، محمد، التجديد بين اللغة والرياضيات في مغرب القرنين 13 و14، ضمن التقليد والتجديد في الفكر العلمي، منشورات كلية الآداب والعلوم الإنسانية بالرباط، ط1، 2003.
• أبلاغ، محمد، وجبار، أحمد: حياة ومؤلفات ابن البنا المراكشي، منشورات كلية الآداب والعلوم الإنسانية بالرباط، ط1، 2001م.
• جبار، أحمد ، العلوم العربية في عصرها الذهبي، ترجمة، عبد السلام الشدادي ومحمد أبلاغ، بيت الفنون والعلوم والآداب،2005.
• صليبا، جميل، المعجم الفلسفي، دار الكتاب اللبناني، 1982م، ج1.
• حاجي خليفة، كشف الظنون، اعتنى به عبد القادر عطا، 7 أجزاء، دار الكتب العلمية، ط1 ،2008.
• الجابري، ادريس النغش، دراسات في فلسفة العلوم الإسلامية وتاريخها، مطبعة آنفو برانت، فاس، ط1، 2009م.
• التادلي ابن هيدور، “التمحيص في شرح التلخيص” دراسة فلسفية وتحليل رياضي وتحقيق، د. ادريس نغش الجابري، أطروحة لنيل شهادة الدكتوراه، كلية الآداب والعلوم الإنسانية بالرباط. 2007م.
• رشدي راشد، موسوعة تاريخ العلوم العربية، الجزء الثاني: الرياضيات والعلوم الفزيائية، نشر مركز دراسات الوحدة العربية ومؤسسة  عبد الحميد شومان، بيروت، ط1، 1997.
• سعد الله ، أبوبكر خالد: من علماء المغرب الإسلامي، الرياضي ابن منعم العبدري، مجلة آفاق الثقافة والتراث، السنة الثالثة عشر، العدد التاسع والأربعون، صفر 1426- أبريل، أبريل نيسان 2005م.
• Lamrabet D ., Introduction à L‘histoire Des Mathématique Magrebins, Lamarif Aljadida, Rabat, 1994.
• Djebbar A.,Une Histoire de la Science arabe. Ed. Le Seuil.Paris.2001.
• Djebbar A : Les mathématique dans le Maghreb impérial du XIIe- XIIIe siécle, in Act du 7^éme colloque Maghrebin sur L’Histoire des Mathématique Arabes, Ecole Normale Supérieure Marrakech, 1^ere édition, 2005. V1.

1ـ انظر: أحمد جبار، العلوم العربية في عصرها الذهبي، ترجمة، عبد السلام الشدادي ومحمد أبلاغ، بيت الفنون والعلوم والآداب، 2005، ص 33

[2]– عالم رياضي وطبيب أندلسي الأصل من مدينة دانية، استقر بمراكش، عايش خلافة الناصر لدين الله (1199-1213) وتوفي بها سنة 626هـ/1228. له ترجمة في الذيل والتكملة لابن عبد الملك المراكشي، السفر الأول، تحقيق محمد بن شريفة، دار الثقافة، بيروت، القسم الأول، (د.ت)، ص59-60.       

[3]– فقه الحساب، تقديم، ادريس لمرابط، دار الأمان، الرباط، الطبعة الأولى، 2005، ص 12.

[4]– فقه الحساب، ص 12.

[5] – نفسه، هامش ص 92.

[6] – نفسه، هامش ص 114.

* ما بين معقوفتين إضافة من المحقق.

[7] – المرجع نفسه، ص 15.              

[8] – نفسه، ص 19.

[9] – نفسه، ص 20

[10] –  نفسه، هامش ص 18.

[11]– نفسه، هامش ص 18.

[12]– نفسه، هامش ص 20.

[13]– نفسه، هامش ص 22.

[14]– نفسه، هامش ص 157.

[15]– نفسه، هامش ص 190.

[16]– نفسه، هامش ص 25.

[17]– نفسه، هامش ص 26.

[18]– نفسه، هامش ص 29.

[19]– في الوجه الأول من الصفحة يضع المحقق الصفحة الأولى والأخيرة من نسخة فقه الحساب. وفي الوجه الثاني من الصفحة الموالية نجد أربع صفحات، الصفحة الأولى تعالج قضايا معجمية بواسطة التحلبل التوافقي، الصفحة الثانية تعالج استخراج الضلع المسبع، الصفحة الثالثة والرابعة تدرس الأشكال العددية دراسة مفصلة. ( المرجع  نفسه، ص 361-362.)  

 [20]– نفس العدد من مجلة آفاق الثقافة والتراث ص، 175.

[21]– ابن منعم العبدري، فقه الحساب، تقديم، إدريس لمرابط، دار الأمان، الطبعة الأولى، 2005م، ص237.

[22]– المصدر نفسه، ص 13.  

[23]– البرهان التحليلي:démonstration analytique هو البرهان الذي نصعد فيه من النتائج إلى المبادئ، أي من القضية المراد إثباتها إلى قضية صادقة أبسط منها. وهذا البرهان بدوره ينقسم إلى قسمين: الأول – البرهان التحليلي المباشر démonstration par récurrence  ويسمى كذلك البرهان بالترجع، الثاني – البرهان التحليلي الغير المباشر démonstration par absurde  ويسمى هذا البرهان بالبرهان بالخلف أو خلاف الفرض.

البرهان التركيبي:démonstration synthétique هذا البرهان عكس التحليل بحيث ننطلق فيه من المبادئ إلى النتائج كالاستنتاج الرياضي الذي تلزم فيه النتيجة من المبادئ اضطرارا والمبادئ هنا هي: البديهيات والتعريفات والمسلمات. ينظر: جميل صليبا، المعجم الفلسفي، ، دار الكتاب اللبناني، 1982م، ج1، ص 207.

[24]– مجلة آفاق الثقافة والتراث، نفس المرجع، ص176.   

[25]–  ابن منعم العبدري، فقه الحساب، تقديم، ادريس لمرابط، ص201.

[26]– المرجع نفسه، ص201.

[27]– أبوبكر خالد سعد الله، من علماء المغرب الإسلامي، الرياضي ابن منعم العبدري، مجلة آفاق الثقافة والتراث، السنة الثالثة عشر، العدد التاسع والأربعون، صفر 1426-أبريل، أبريل نيسان 2005م، ص 174.

[28]– الذيل والتكملة، السفر الأول، تحقيق محمد بن شريفة، دار الثقافة، بيروت، القسم الأول، (د.ت)، ص59-60.      

[29]– ابن هيدور، تحفة الطلاب وأمنية الحساب في شرح ما أشكل من رفع الحجاب، مخ. الفاتيكان، 20ظ-21و. تم ذكرها في كتاب: حياة ومؤلفات ابن البنا المراكشي، أحمد جبار- محمد أبلاغ، منشورات كلية الآداب والعلوم الإنسانية، ط1، 2001. ص 54.

[30]–  ابن خلدون، المقدمة، حققها وقدم لها وعلق عليها عبد السلام الشدادي، 5مج، خزانة ابن خلدون بيت الفنون والعلوم والآداب، 2005، ج3، ص80. 

[31]– حاجي خليفة، كشف الظنون، اعتنى به عبد القادر عطا، دار الكتب العلمية، ط1 ،2008 ، ج2، ص 523.

[32]– من أهم أعمال هؤلاء يمكن أن ننظر منها بالتحديد:

محمد أبلاغ – أحمد جبار، حياة ومؤلفات ابن البنا المراكشي، منشورات كلية الآداب والعلوم الإنسانية بالرباط، ط1، 2001، ص31.

• Djebbar A.,Une Histoire de la Science arabe. Ed. Le Seuil.Paris.2001.pp 230-237.
• Djebbar A : Les mathématique dans le Maghreb impérial du XIIe- XIIIe siécle, in Act du 7^éme colloque Maghrebin sur L’Histoire des Mathématique Arabes, Ecole Normale Supérieure Marrakech, 1^ere édition, 2005. V1. pp 118-121.

[33]– الجابري، ادريس النغش، دراسات في فلسفة العلوم الإسلامية وتاريخها، مطبعة آنفو برانت، فاس، ط1، 2009م. ص 126.

[34]– فرع من فروع الرياضيات، يُعنى بالتعداد، أي بتحديد العناصر والمجموعات الجزئية المتمتعة بخصائص معينة داخل مجموعة معطاة. ويرتبط التحليل التوافقي بنظرية الأعداد ونظرية البيانات. وقد كانت طرقه  من قبل مبنية بهدف حل مسائل محددة، فظهر كأداة رياضية تُسْتَعْمل في حالات متعددة: لغوية وفلسفية ورياضية، وقد تجلى هذا النشاط عند كل من اللغويين والفلاسفة اللذين طرحوا مسائل تتعلق باللغة في ثلاث ميادين خاصة منها: علم النطقيات والمعجميات وعلم الرموز. ينظر: رشدي راشد، “التحليل التوافقي، التحليل العددي التحليل الديوفنطسي ونظرية الأعداد”، في موسوعة تاريخ العلوم العربية، الجزء الثاني: الرياضيات والعلوم الفزيائية، نشر مركز دراسات الوحدة العربية ومؤسسة عبد الحميد شومان، بيروت، ط1، 1997، ص 491 – 498.   

[35]– إن أعمال اللغوي الكبير الخليل بن أحمد الفراهيدي كانت هي الأصل الأول الذي من خلاله برزت المساهمة اللغوية في ميلاد التحليل التوافقي، حيث أنه أعد المعجم العربي وفق طريقة ترتيبية Arrangements وتوافقية combinatoire. ينظر: محمد أبلاغ، التجديد بين اللغة والرياضيات في مغرب القرنين 13 و14، ضمن: التقليد والتجديد في الفكر العلمي، منشورات كلية الآداب والعلوم الإنسانية بالرباط، ط1،2003، ص89-90.  

[36]– “التمحيص في شرح التلخيص” دراسة فلسفية وتحليل رياضي وتحقيق، د.ادريس النغش الجابري، أطروحة لنيل شهادة الدكتوراه، كلية الآداب والعلوم الإنسانية بالرباط،2007، ص 152. =

[37]– Lamrabat driss: Introduction a L‘histoire Des Mathématique Magrebins, Lamarif Aljadida, Rabat, 1994, p.73.

[38]–  ipd.,p,73.

[39]– أحمد جبار، العلوم العربية في عصرها الذهبي، ترجمة، عبد السلام الشدادي ومحمد أبلاغ ، بيت الفنون والعلوم والآداب،2005، ص.41.